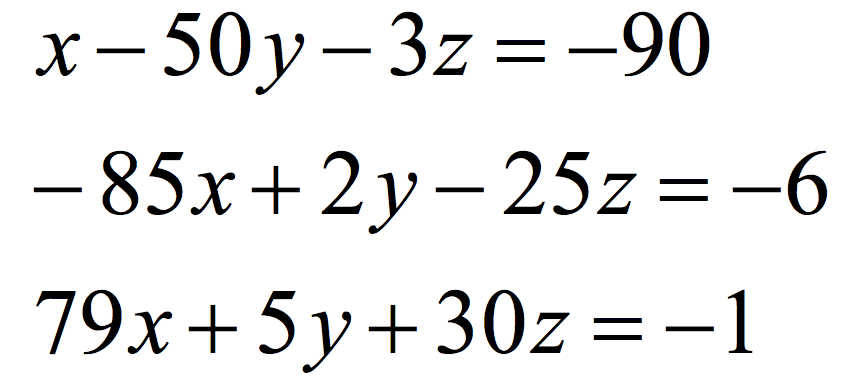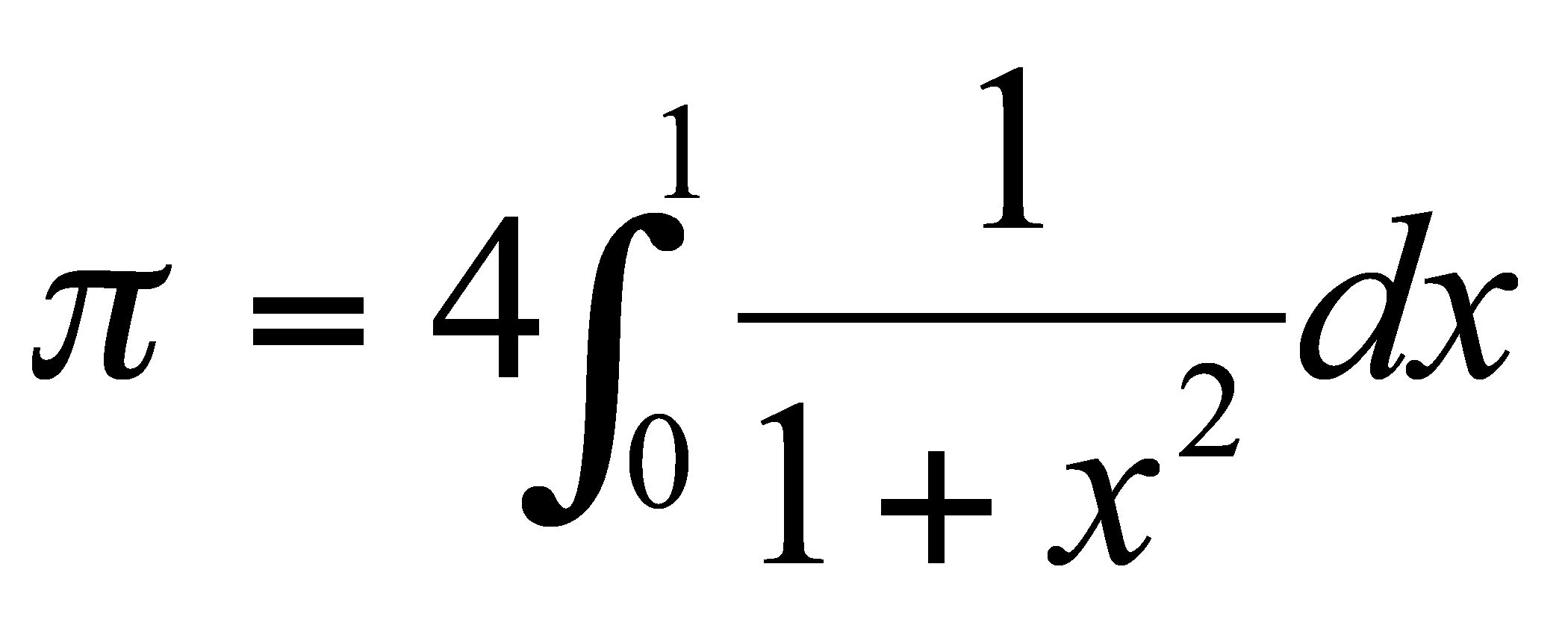
def f(x)
x/((x+1.0)*(x+2.0))
end
def trapezoid(xs,xe,n)
deltax = (xe-xs)*1.0/n
sum = (f(xs)+f(xe))/2.0
for i in 1..(n-1)
sum = sum + f(xs+i*deltax)
end
deltax * sum
end
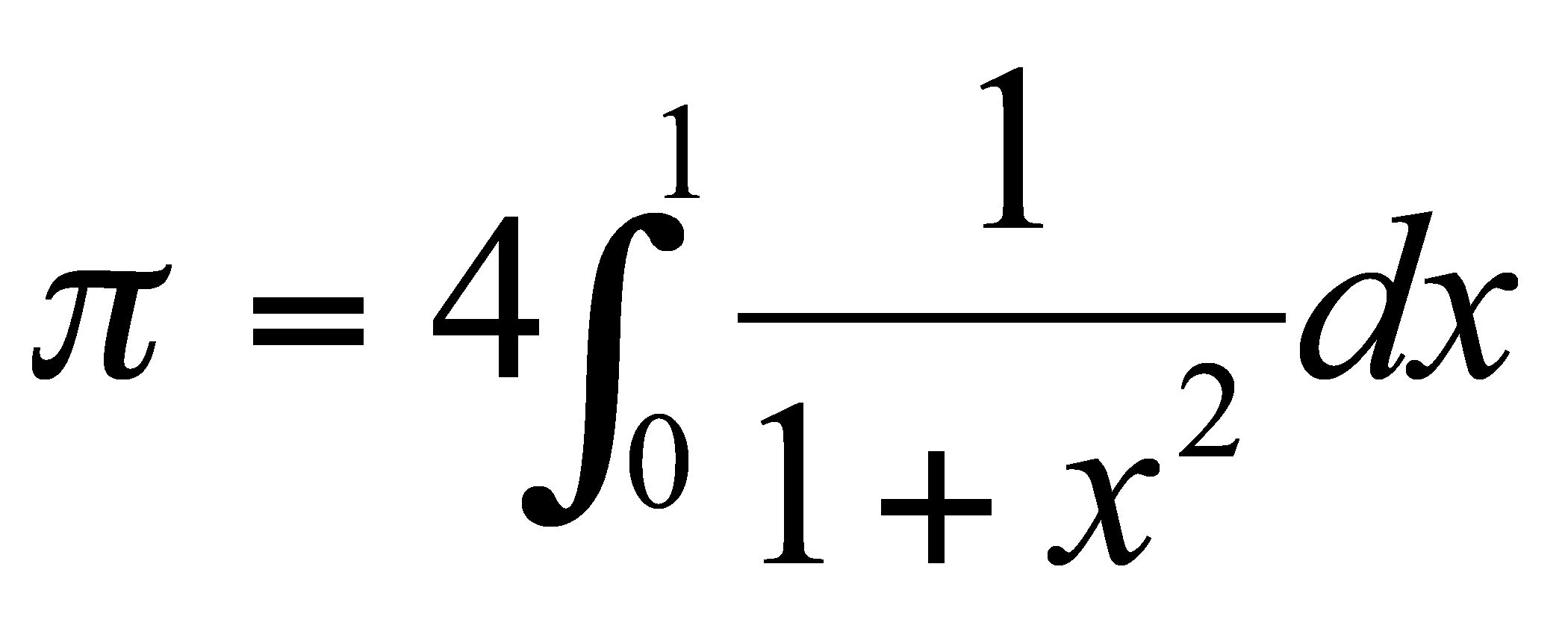
def pi(n) 4.0 * trapezoid(....) end
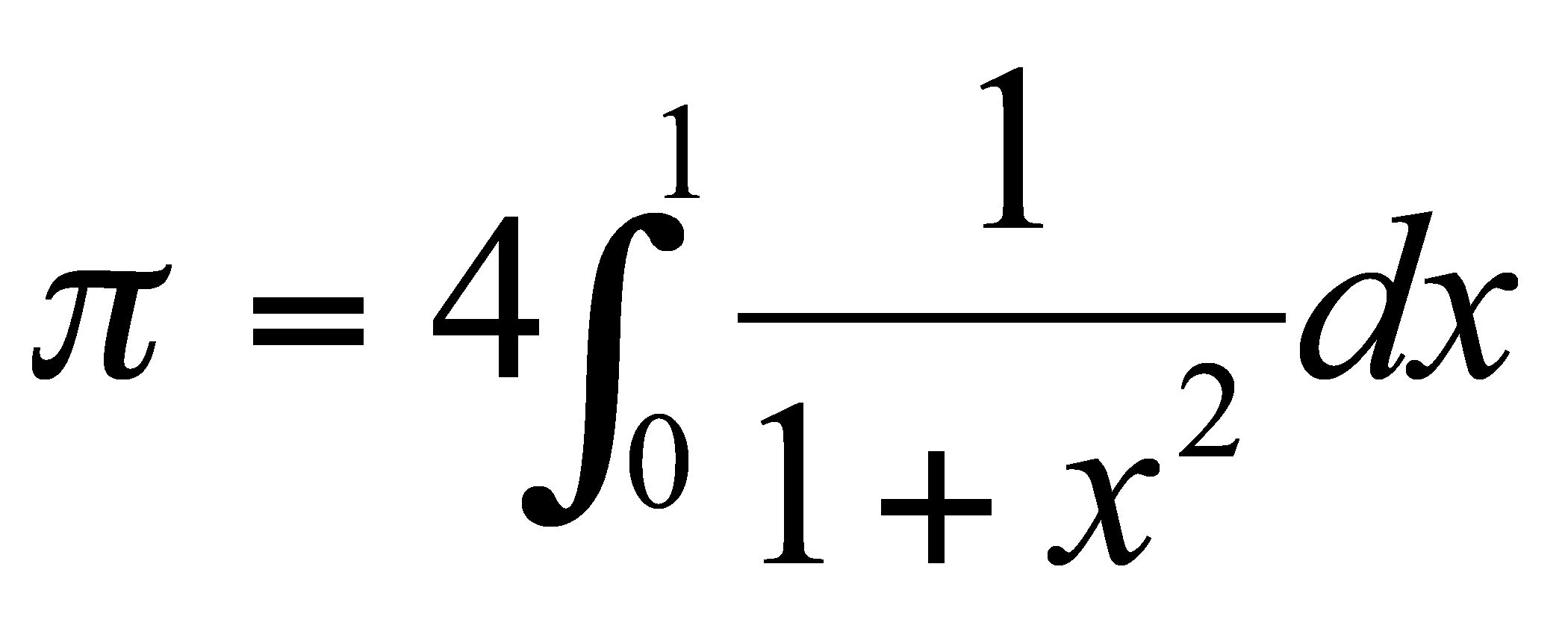
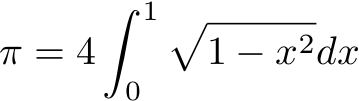
def montecarlo(n)
m=0
for i in 1..n
x=rand() # random number in [0,1)
y=rand()
if x*x + y*y < 1.0
m = m + 1
end
end
m*1.0/n
end
def mcplot(n)
a = make2d(500,500)
for i in 1..n
x= rand() # random number in [0,1)
y= rand()
if x*x + y*y < 1.0
a[y*500][x*500] = 1.0
else
a[y*500][x*500] = 0.5
end
end
a
end
0 01111111 10000000000000000000000(単精度表現)
0 10000000 10000000000000000000000(単精度表現)
0 01111110 00000000000000000000000(単精度表現)
0 00000000 00000000000000000000000(単精度表現)
def gj(a) # Gauss-Jordan method without pivoting
row = a.length()
col = a[0].length()
for k in 0..(col-2)
akk = a[k][k]
for i in 0..(col-1) # normalize row k
a[k][i]=a[k][i]*1.0/akk
end
for i in 0..(row-1) # eliminate column k
if i != k # of all rows but k
aik = a[i][k]
for j in k..(col-1)
a[i][j] = a[i][j] - aik * a[k][j]
end
end
end
end
a
end
def maxrow(a,k)
#a[i][k]の絶対値が最大となるi>=kを探す
end
def swap(a,i,j)
tmp=a[i]
a[i]=a[j]
a[j]=tmp
end
def gjp(a) # Gauss-Jordan method WITH pivoting
row = a.length()
col = a[0].length()
for k in 0..(col-2)
max=maxrow(a,k) # find absolute-maximal coeff.
swap(a,k,max) # swap rows
akk = a[k][k]
for i in 0..(col-1) # normalize row k
a[k][i]=a[k][i]*1.0/akk
end
for i in 0..(row-1) # eliminate column k
if i != k # of all rows but k
aik = a[i][k]
for j in k..(col-1)
a[i][j] = a[i][j] - aik * a[k][j]
end
end
end
end
a
end
ヒント: 「式1」の絶対値は「式1.abs()」で得られる.(例)
irb(main):002:0> x=3 => 3 irb(main):003:0> (x-4).abs() => 1