turtleライブラリ
turtleライブラリは、ペンをもった「カメ」を操作することで絵を書くためのライブラリです。このようなシステムは「タートルグラフィックス」と呼ばれ、プログラミングの入門教材として広く使われています。
プログラミング例
以下のプログラムは、その左にあるような星印を描きます。

import turtle
turtle.setup()
turtle.pendown()
for i in range(0,5):
turtle.forward(100)
turtle.right(144)
turtle.penup()
import turtleはturtleライブラリの読み込みです。また、turtle.setup()はカメが動き回るキャンバスの起動です。この2行は1度だけ実行すれば大丈夫です。
注意:Google Colabを使っている人は、上記2行の代わりに以下の3行を実行してください。
!pip install ColabTurtle import ColabTurtle.Turtle as turtle turtle.initializeTurtle()
カメはペンをもっています。turtle.pendown()関数を呼ぶと、カメはペン先を紙につけます。以降、カメが動いた軌跡が描画されます。一方、turtle.penup()関数を呼ぶと、カメはペン先を紙から離します。
今回の例では、カメは「前へ100進む(turtle.forward(100))」と「144度右を向く(turtle.right(144))」を5回繰り返すことで、星を描いています。
turtleライブラリの主な機能
turtleライブラリの主な機能は以下のとおりです。もっと詳しい情報を知りたい場合、リファレンスマニュアルを見てください。
- turtle.forward(d)
カメが向いている方向に距離d進みます。 - turtle.right(a)
カメが右にa度回転します。 - turtle.left(a)
カメが左にa度回転します。 - turtle.goto(x, y)
カメが座標(x,y)に移動します。turtle.forwardと同様、ペンが紙に付いていた場合、軌跡は描かれます。 - turtle.setheading(a)
カメがa度方向を向きます。真東が0度、真北が90度、真西が180度、真南が270度です。 - turtle.pendown()
ペン先を紙につけます。以降カメの移動の軌跡が描かれます。 - turtle.penup()
ペン先を紙から離します。以降カメの移動の軌跡は描かれません。 - turtle.pencolor(c)
ペンで描かれる軌跡の色をcにします。 - turtle.reset()
初期状態に戻ります。具体的には、カメが初期位置に戻り、 今まで描いた軌跡が全て消えます。
演習課題例
流れ星
流れ星を1つ描く関数を作り、それをfor文で何度も呼ぶことにより、下のような流れ星を描くプログラムを書け。

うずまき
- 一辺の長さdの正n角形を描く関数polygon(d,n)をプログラムせよ。
- polygon(d,n)のnを十分大きくすると円が描ける。これを利用して、半径rの円を描く関数circle(r)をプログラムせよ。
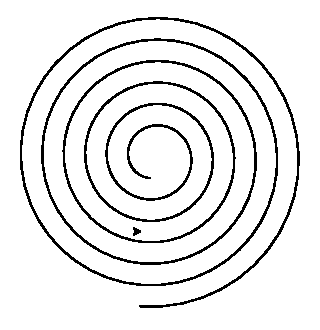
ヒント:mathライブラリを利用しよう。 - circle(r)と同様にして、半径が徐々に小さくなるように描くと渦巻きになる。これをふまえ、下のような渦巻きを描くプログラムを作成せよ。
フラクタル
- 正三角形を描くプログラムを作れ。
- 正三角形の各辺の中心に1/3の大きさの正三角形を付け加えたような、下左端の図形を描くプログラムを作れ。
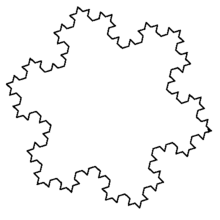
- 同様に、各辺の中心にその辺の1/3の大きさの正三角形を付け加えることを繰り返し、下右のような図形を描くプログラムを作れ。
ヒント:再帰関数を用いる。0段階目が正三角形、1段階目が(1)で作った図形……として段階を増やしてゆくことを考える。下図は右に進むに従い1段階ずつ段階が上がっている。このとき、n段階目の「一辺」は、n+1段階目の「一辺」を4つ組み合わせたものになる。



積分
関数fと数値hに対し「現在地点 (x, y) から (x + h, y + h × f(x)) まで移動しつつ線を引く」ことを繰り返すことを考える。hが小さければ、描かれる線は関数fを積分して得られる関数に対応すると思われる。これを以下のように実現せよ。- (dx, dy) が与えられた時、現在地点を (x, y) として、現在地点から (x + dx, y + dy) へまっすぐカメを動かすプログラムを作れ。
ヒント:カメが今どちらを向いているかに結果が影響されてはいけない。 - 常識的な関数の入力・出力の値はそのままカメの位置として使うには適していない。「関数の入出力値をscale倍した値がカメの座標」となるような変数scaleを適当に定めよ。
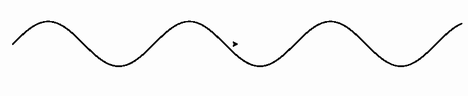
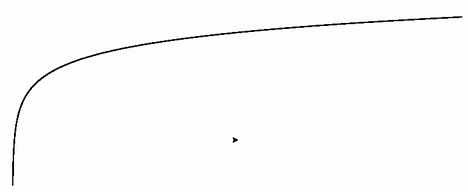
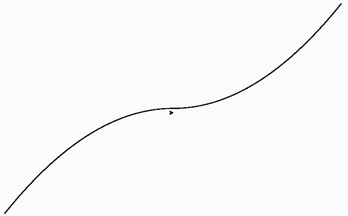
- 「現在地点 (x, y) から (x + scale × h, y + scale × h × f(x / scale)) まで移動しつつ線を引く」ことを繰り返すプログラムを作れ。なお、下図左上はcos関数を、左下はf(x) = 1/xを、右はf(x) = |x| / 4を、それぞれこの手法で積分した結果である。
- (発展課題)この手法での積分の精度を評価するため、厳密な積分結果が分かっている適当な関数(例えばf(x) = 1/x)についてこの手法を適用し、厳密な積分結果をプロットしたものと比較せよ。また、「h × f(x)」の部分を「h × (f(x) + f(x + h)) / 2」とするとどうなるかもためしてみよ。